Best Sudoku Strategies: Tips for Every Skill Level

Are you looking to improve your Sudoku skills? Whether you’re a beginner struggling with the basics or an expert seeking advanced techniques, mastering effective Sudoku strategies can transform your gameplay from frustrating to fulfilling.

In this comprehensive guide, we’ll explore the best Sudoku strategies for every skill level, from fundamental techniques to expert-level tactics that will help you solve even the most challenging puzzles. You’ll discover how to approach Sudoku systematically, avoid common pitfalls, and develop the analytical thinking that makes solving these number puzzles both enjoyable and rewarding.

How to win Sudoku: strategies for beginners! 

New to Sudoku? Don’t worry—everyone starts somewhere! These fundamental techniques will help you build a solid foundation and develop the mindset needed to tackle more complex puzzles.

The scan and cross-hatching technique

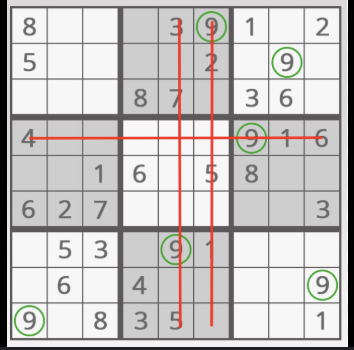
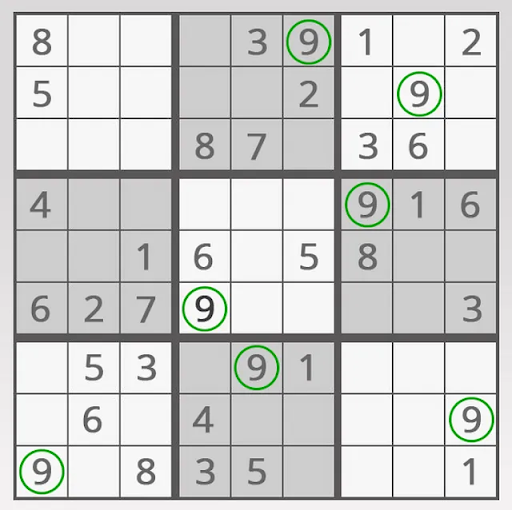
The scan technique is often the first strategy every Sudoku player learns. It involves systematically scanning rows, columns, and boxes to identify where a specific number can be placed.

To use this technique effectively:

1. Select a number (going in order makes it easier).
2. Scan each row and column to see where that number already appears.
3. For each 3×3 box that doesn’t contain your chosen number, identify eligible cells by eliminating positions that conflict with existing numbers in related rows and columns.

Cross-hatching takes scanning a step further by looking for cells that have only one possible value. When scanning horizontally and vertically, if only one empty cell remains in a row, column, or box where a certain number can go, then that number must go in that cell.

This technique is particularly effective for easier puzzles and serves as the foundation for more advanced strategies.

The Only Candidate (Naked Singles)

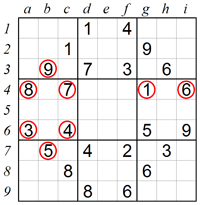
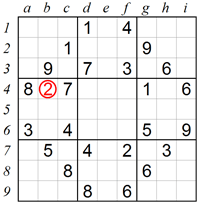
The Only Candidate strategy, also known as “Naked Singles,” focuses on finding cells that can only contain one possible number. When a cell has only one possible value after eliminating all other options based on the numbers present in its row, column, and box, that number must go into the cell.

For example, if a cell can’t contain numbers 1-8 because they already appear in its row, column, or box, then the cell must contain 9.

This approach is straightforward but remarkably effective, especially in the early stages of solving a puzzle. It requires careful observation rather than complex logic, making it perfect for beginners.

The Hidden Single

While the Only Candidate strategy focuses on cells with only one possibility, the Hidden Single strategy looks at numbers that can only go in one place within a row, column, or box.

For instance, if the number 5 can only be placed in one specific cell within a box (even though that cell might accept another number too), then 5 must go in that cell.

This technique is slightly more advanced than the previous ones because it requires you to track possibilities for each number rather than for each cell.

Pencil Marks (Candidate Listing)

As puzzles become more challenging, keeping track of possible values for each cell becomes essential. This is where pencil marks come in. Instead of immediately filling in definite values, you note all possible numbers a cell could contain.

Use the previous strategies to try and narrow down to just a few numbers that could go in each cell (ideally two or three). Write them down with a pencil within the cell so that you can keep them as a reference for later. 

When you use the previous strategies but still cannot determine what number goes in a specific cell, but have a few guesses, you can write them down to keep them as a reference for later. You may be able to use these when comparing to other cells where you cannot make an ultimate decision.

Careful! Some common mistakes to avoid 

Even with these foundational strategies, beginners often fall into predictable traps:

• Rushing to fill in numbers: Take your time to analyze the board thoroughly.
• Forgetting to update pencil marks: When you place a number, remember to update all affected pencil marks.
• Overlooking simple opportunities: Sometimes, the easiest moves are hidden in plain sight.
• Guessing: While trial and error can work, logical deduction is more reliable. Keep guessing as a las resource.
• Focusing too much on one area: Scan the entire grid regularly to avoid missing obvious moves.

Remember, Sudoku is about patience and systematic thinking. Build your skills gradually, and don’t be discouraged if you need to use hints occasionally. Every puzzle you complete improves your abilities for the next challenge.

5 intermediate Sudoku tactics

Once you’ve mastered the basics, these intermediate strategies will help you tackle more challenging puzzles and develop deeper analytical skills.

1) The Pointing Pairs and Triples method

The Pointing Pairs and Triples strategy comes into play when a specific number can only appear in two or three cells within a box, and these cells happen to align in the same row or column.

When this occurs, that number can be eliminated as a possibility from all other cells in that shared row or column outside the box since it must appear in one of the identified cells.

For example, if the number 4 can only appear in two cells that share a row within a 3×3 box, then 4 cannot appear anywhere else in that row outside the box.

This technique creates powerful chain reactions, eliminating possibilities across the grid and often revealing cells with only one possible value.

2) The X-Wing strategy 

The X-Wing is an elegant strategy that occurs when a candidate number appears in exactly the same two positions in two different rows. These four cells form a rectangle (or an “X” if you draw diagonal lines connecting them).

When this pattern occurs, the candidate number must be placed in two of these four positions—in opposing corners. For example, if a certain number can only appear in two specific positions in two different rows, you know that the number must occupy two of the four corners of the resulting rectangle.

This means you can eliminate that number as a possibility from any other cells that share the same columns as these four cells. The same logic applies if you find the pattern in columns instead of rows.

The X-Wing creates a powerful constraint that can break through seemingly impossible puzzles. While X-Wings are relatively rare, they’re worth looking for when you get stuck, as they often create breakthrough moments in difficult puzzles.

3) The Box-Line Reduction method

Box-Line Reduction is the inverse of the Pointing Pairs strategy. Instead of looking at how cells within a box can eliminate candidates from a line, it examines how candidates restricted to a particular line within a box can be eliminated from the rest of the box.

If a specific number can only appear in cells that share a row or column within a box, then that number cannot appear elsewhere in the box.

This technique often goes unnoticed but can be tremendously effective in removing candidates and simplifying the puzzle.

4) The Naked Pairs, Triples, and Quads strategy

The Naked Pairs strategy comes into play when two cells in the same row, column, or box contain the exact same two candidate numbers and no others. Since these two numbers must go into these two cells, they can be eliminated as possibilities from all other cells in the shared row, column, or box.

For example, if two cells in the same row can only contain the numbers 2 and 7 (we don’t know which cell gets which number), then we know for certain that 2 and 7 will occupy those cells. This means 2 and 7 can be eliminated as candidates from all other cells in that row.

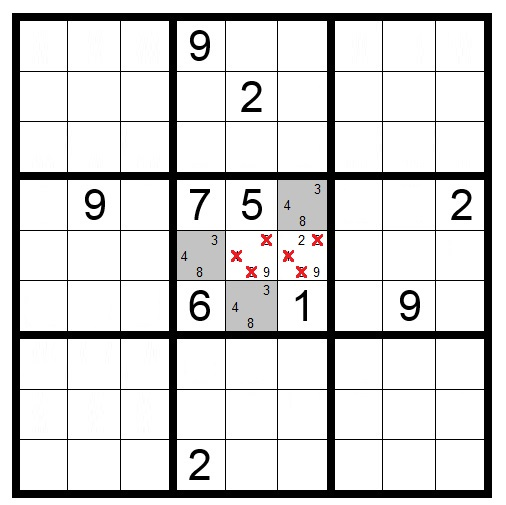
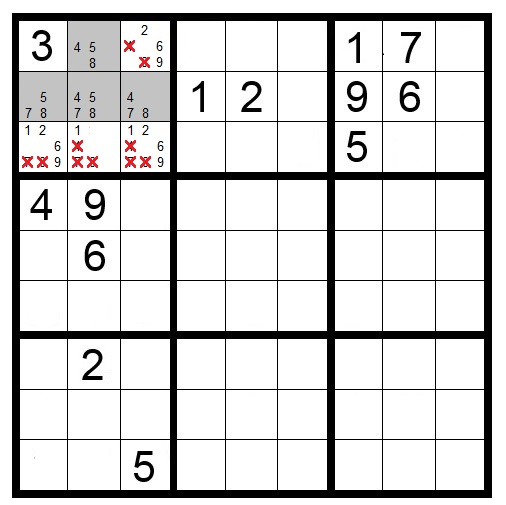
This concept extends to Naked Triples (three cells sharing the same three candidates) and Naked Quads (four cells sharing the same four candidates). Importantly, not all cells need to contain all the candidate numbers. For instance, a Naked Triple might have cells containing (1,5), (1,8), and (5,8)—together, they contain exactly three numbers that must go into those three cells.

The power of this strategy lies in its ability to eliminate possibilities without actually solving any cells directly, often creating chain reactions that reveal new Naked Singles or Hidden Singles.

5) The Hidden Pairs Triples and Quads strategy

Hidden Pairs occur when two numbers can only be placed in the same two cells within a row, column, or box, even though these cells may contain other candidates as well.

For example, if you examine a row closely and notice that candidates 1 and 4 appear only in two specific cells, even though those cells might also contain other candidates like 6 or 9, you’ve found a Hidden Pair. Since 1 and 4 must go into those two cells, you can eliminate all other candidates from these cells.

The key difference between Hidden and Naked Pairs is that Hidden Pairs are obscured by additional candidates in their cells, making them harder to spot. You need to look at the distribution of each candidate number across a row, column, or box to find them.

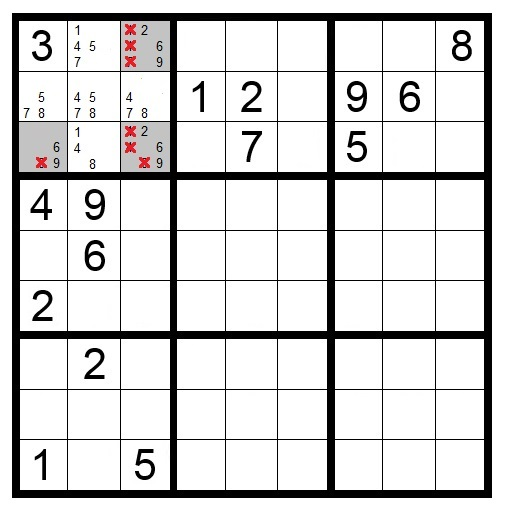
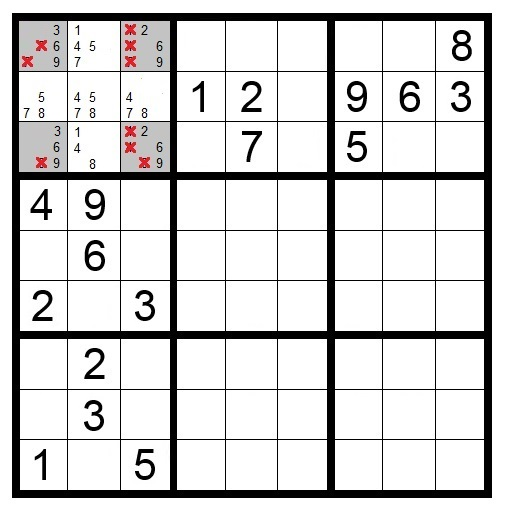
Like their Naked counterparts, Hidden Pairs extend to Triples and Quads, following the same principle but with increasing complexity.

This strategy often reveals new Naked Singles or other patterns, creating a cascade of solved cells that can break through seemingly impossible puzzles.

Careful! Some common mistakes to avoid

Intermediate players should watch out for these common pitfalls:

• Misidentifying patterns: Double-check your patterns before making eliminations.
• Forgetting to update candidates: After applying a strategy, update all affected cells.
• Overlooking simpler strategies: Sometimes, a basic technique will work when you’re focused on complex patterns.
• Becoming fixated on one strategy: Be flexible and willing to switch approaches.
• Losing track of the big picture: Remember that the goal is to solve the puzzle, not just apply fancy techniques.

As you practice these intermediate strategies, you’ll develop an intuition for when to apply each one, making your solving process more efficient and enjoyable.

11 advanced Sudoku strategies

Ready to tackle the hardest Sudoku puzzles? These advanced strategies will give you the tools to conquer even the most challenging grids.

Swordfish

Swordfish is an extension of the X-Wing pattern, involving three rows and three columns. When a candidate number appears in only 2-3 cells in each of three different rows, and these cells are restricted to three specific columns, the candidate can be eliminated from all other cells in those three columns.

Think of it as an X-Wing expanded to three rows and three columns. The name comes from the pattern resembling a swordfish when lines are drawn connecting the cells.

This technique is powerful but requires careful observation to identify, as it creates a more complex grid pattern than the X-Wing’s simple rectangle. While rare, spotting a Swordfish can lead to significant breakthroughs in difficult puzzles that otherwise seem unsolvable.

Jellyfish

Taking the pattern one step further, Jellyfish involves four rows and four columns. Like Swordfish, it allows for eliminations when a candidate is restricted to specific positions, forming a recognizable pattern.

Due to its complexity, Jellyfish is rarely needed for all but the most difficult puzzles, but understanding its logic helps develop advanced pattern recognition skills.

XY-Wing

The XY-Wing strategy involves three cells: a pivot cell with two candidates (XY) and two wing cells that each share one candidate with the pivot and have one other candidate in common (XZ and YZ).

For instance, suppose a central cell contains only two possible numbers. It connects to two other cells, each sharing one number with the central cell, while both wing cells share a different common number. This creates a logical constraint: no matter which value goes into the pivot cell, one of the wing cells must contain their common value.

Therefore, that common value can be eliminated from any cell that shares a row, column, or box with both wing cells.

This technique creates powerful eliminations that often break through seemingly impossible puzzles, especially when you’ve already eliminated many candidates and the cells are down to just two or three possibilities.

XYZ-Wing

XYZ-Wing is a variation of XY-Wing where the pivot cell contains three candidates (XYZ) instead of two. The wing cells still share candidates with the pivot (XZ and YZ), and the elimination works the same way.

This subtle variation increases the number of patterns you can identify and leverage.

W-Wing

W-Wing involves two cells that both contain the same two candidates, connected by a strong link (a situation where if one value isn’t in a cell, it must be in another). When such a pattern is identified, certain eliminations become possible.

This technique requires understanding strong and weak links, representing a significant step up in complexity.

Remote Pairs

Remote Pairs occur when you have a chain of cells, each containing the same two candidates, with strong links between them. This creates a situation where cells at both ends of the chain must contain different values, enabling eliminations.

This strategy tests your ability to track relationships across the entire grid, a hallmark of advanced Sudoku solving.

Chains (Alternating Inference Chains – AIC)

Alternating Inference Chains track logical connections between candidates across the grid. They work by following a series of logical “if-then” statements that create a chain of implications.

These chains work on a simple principle: if a candidate must be in one of two cells, and one of those cells forces another candidate placement elsewhere, you can follow the chain of logical consequences. If that chain eventually creates a contradiction or circles back to impact cells at the beginning of the chain, you can make eliminations.

AICs can be built on strong links (if X is not here, it must be there) and weak links (if X is here, it cannot be there). By alternating between these links, you can create powerful chains of logical deductions.

AICs represent one of the most powerful techniques in advanced Sudoku solving, but they require careful tracking and logical reasoning. Many solvers use colored pencils or notation systems to keep track of these chains.

Coloring (Simple & Multi-Coloring)

Coloring involves assigning colors to candidates in chains of cells, where each color represents a possible solution state. It’s particularly useful when a candidate appears exactly twice in each row, column, or box, creating a chain of alternating possibilities.

The basic idea is to pick a number that forms strong links throughout the grid. Starting with one cell containing that number, color it (for example, blue). Then, if that cell contains the number, other cells in the same row, column, or box cannot contain it—so the next possible position gets colored differently (say, orange). Continue alternating colors as you follow the chain of possibilities.

If you ever find two cells of the same color in the same row, column, or box, you’ve discovered a contradiction—that coloring scheme is impossible, so the opposite coloring must be correct. Alternatively, if a cell can see both colors, then that cell cannot contain the number you’re tracking.

This technique transforms abstract logical relationships into a visual system, making complex deductions more manageable. Many expert solvers consider it essential for the hardest puzzles.

Unique Rectangle

The Unique Rectangle strategy prevents a specific type of puzzle ambiguity by identifying potential “deadly patterns” where multiple solutions could exist. Well-designed Sudoku puzzles have only one solution, which we can leverage in our solving technique.

If you find four cells forming a rectangle (with corners in two rows and two columns) that contain the same pair of candidates, this could lead to multiple solutions. In such cases, if one of the four cells contains additional candidates, those extra candidates must be the correct value for that cell, as this prevents the ambiguous rectangle from forming.

This technique not only helps solve the puzzle but also provides insight into puzzle construction and logical constraints that ensure a unique solution. It’s particularly useful in advanced puzzles that have been carefully crafted to have exactly one solution.

Finned X-Wing & Finned Swordfish

These are variations of the standard X-Wing and Swordfish patterns with additional “fins”—extra cells that modify how the eliminations work. Recognizing these patterns requires advanced pattern recognition skills but provides powerful elimination opportunities.

The Kraken X-Wing

The Kraken X-Wing combines the X-Wing pattern with chains of implications, creating one of the most complex and powerful techniques in Sudoku solving. Reserved for only the most challenging puzzles, mastering this technique represents a significant achievement.

Careful! Some common mistakes to avoid

Even experienced solvers should watch out for these pitfalls:

• Overcomplicated analysis: Sometimes, simpler techniques work when you’re looking for complex patterns.
• Confirmation bias: Don’t force patterns where they don’t exist.
• Calculation errors: With complex techniques, double-check your logic.
• Strategy overreliance: Maintain flexibility in your approach.
• Losing perspective: Remember that solving should be enjoyable, not frustrating.

As you master these advanced techniques, you’ll find that even the most diabolical puzzles become conquerable with patience and systematic analysis.

5 Sudoku tips and tricks for proclaimed experts

For those who have mastered advanced techniques, these expert-level strategies represent the pinnacle of Sudoku-solving skill.

1) Did you know… the Sue de Coq technique?

Named after a Sudoku forum user, Sue de Coq is a complex elimination technique based on set theory. It involves identifying cells where specific candidates must be distributed in a certain way, allowing for powerful eliminations.

This technique requires understanding how candidates must be allocated across cells, creating constraints that propagate throughout the grid.

2) The Almost Locked Sets (ALS) methods

Almost Locked Sets occur when a group of n cells contains n+1 candidates. These structures create powerful constraints that can be leveraged for eliminations when they interact with other sets.

ALS techniques include ALS-XZ, ALS-Wing, and ALS chains, each providing sophisticated ways to identify and exploit these nearly locked candidate sets.

3) Death Blossom

The Death Blossom technique involves a central cell (the stem) connected to multiple Almost Locked Sets (the petals). By analyzing how candidates must be distributed across this structure, certain eliminations become possible.

This visually distinctive pattern represents one of the most elegant solving techniques, though it rarely appears in most puzzles.

4) SK Loop

SK (Single-digit Kraken) Loops involve complex chains of implications focused on a single digit. By tracing how a digit must be placed throughout the grid, contradictions or forced placements can be identified.

This technique tests the limits of logical deduction and requires exceptional attention to detail.

5) Tabling & Forcing Techniques

Tabling involves systematically tracking all possible solutions for a section of the grid to identify contradictions or forced values. Forcing techniques similarly explore the implications of placing a value to see if it leads to contradictions.

These approaches represent the boundary between logical deduction and trial-and-error, requiring both systematic analysis and an intuitive understanding of the puzzle’s structure.

Though forcing techniques can refer to simply testing to see how a certain number would impact the entire grid, there are several techniques to do so, including the Digit Forcing Chain, the Nishio Forcing Chain, and the Unit Forcing Chain.

Careful! Some common mistakes to avoid

At the expert level, these pitfalls can still trip up the most experienced solvers:

• Exhaustion and carelessness: Complex techniques require mental endurance.
• Missing simpler solutions: Don’t overlook basic strategies while hunting for complex patterns.
• Overconfidence: Even experts make mistakes in their analysis.
• Technique misapplication: Ensure you fully understand a technique before applying it.
• Losing the joy of solving: Remember why you enjoy Sudoku—for the satisfaction of the solve, not just the technique application.

These expert techniques represent the culmination of Sudoku-solving skill, allowing you to tackle even the most diabolical puzzles with confidence.

Fun variations of Sudoku to try

Looking for new challenges? These Sudoku variations offer fresh twists on the classic puzzle format. Whether you’re seeking a different level of difficulty or just want to spice up your Sudoku experience, there’s something here for everyone.

Monopoly Sudoku

Combine the strategic property management of Monopoly with the logical challenge of Sudoku!

• Main Features: In Monopoly Sudoku, you’ll solve Sudoku puzzles to earn dice rolls, buy properties, and build houses in this unique hybrid game.
• Ideal for users who like playing campaign-based games and board-game lovers

Pogo Daily Sudoku

Never run out of puzzles with Pogo Daily Sudoku! Get a fresh, challenging puzzle every day to keep your skills sharp and track your solving progress over time.

• Main features: Daily puzzles to put your brain to the test every day
• Ideal for users who love a daily challenge to keep their brains trained

Pogo Sudoku

For a classic Sudoku experience with a user-friendly interface, look no further than Pogo Sudoku. 

• Main features: classic sudoku in a virtual environment
• Ideal for users who are just looking for a digital version of the traditional sudoku game

Master Sudoku on Pogo – Start Playing Now!

FAQs 

What is the best Sudoku strategy?

The best Sudoku strategy depends on your skill level and the difficulty of the puzzle. Beginners should master scanning, cross-hatching, and the Only Candidate technique before progressing to more advanced strategies. For most puzzles, a combination of techniques is necessary, starting with the simplest and progressing to more complex ones as needed.

What is the rule of 3 in Sudoku?

The “rule of 3” in Sudoku refers to the fact that each row, column, and 3×3 box must contain all numbers from 1 to 9 without repetition. This fundamental constraint creates the logical framework that makes Sudoku puzzles solvable through deduction rather than guesswork.

Is there a trick to solving Sudoku?

While there’s no single trick that works for all puzzles, the systematic application of solving techniques is key. Starting with pencil marks to track possibilities, then applying techniques like Singles, Pairs, and X-Wings in order of complexity will solve most puzzles. The trick is knowing which technique to apply when, which comes with practice.

Is there a pattern to Sudoku?

Each Sudoku puzzle is unique, but they all follow the same basic rules and can be solved using similar logical techniques. Well-designed puzzles are balanced to provide a satisfying solving experience, requiring a combination of techniques rather than a repetitive application of a single strategy.

What is the hidden rule in Sudoku?

There isn’t a universally acknowledged “hidden rule” in standard Sudoku, but some might refer to uniqueness principles as hidden rules. These principles state that a properly designed Sudoku puzzle has only one solution, which allows for techniques like the Unique Rectangle strategy that exploit this constraint.

What is the magic number in Sudoku?

The “magic number” in Sudoku is 45, which is the sum of all digits from 1 to 9. This property can sometimes be useful in solving certain Sudoku variants like Killer Sudoku, where cells are grouped and must sum to a specified total.